Technical Blog: Quantum Art achieves 10X circuit depth compression
Quantum computers have the potential to significantly improve computational tasks across a wide range of scientific and technological fields. Meaningful quantum advantages are already possible, but they require careful alignment between hardware capabilities and algorithm design.
Quantum circuit synthesis and compilation are critical components in this process, both for contemporary quantum systems, where efficient use of limited resources, such as the number of entangling operations, is essential before errors dominate performance, as well as for large-scale fault-tolerant platforms, where computation time can be significantly reduced.
The specific characteristics of the quantum hardware determine which circuit designs and optimizations are feasible. Optimizing quantum circuits is therefore essential to achieve the best performance.
At Quantum Art we utilize multi-qubit(MQ) gates to compile quantum circuits more efficiently. These gates can create multiple qubit interactions at the same time, unlike standard two-qubit gates that work sequentially. This parallelism compresses the circuits and can speed up computations significantly.
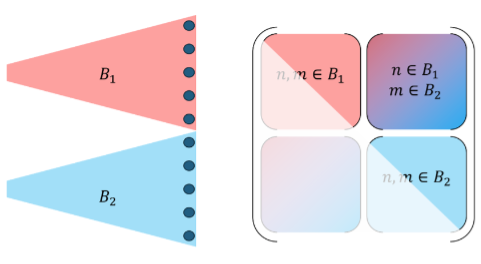
Our gates implement simultaneous, programmable Z ⊗ Z between all qubit-pairs in the register. Formally, given by the logical operator:
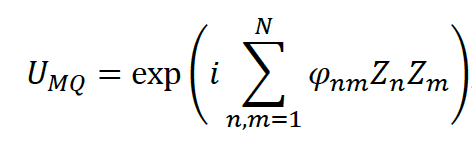
with φ 𝒪(𝑁2) encoding all the pairwise operations, arbitrarily defined by the users.
In practice, this means that any pair of qubits can interact in a programmable manner, simultaneously, throughout the entire register, as shown in the sketch:

MQ gates are naturally available in trapped-ion quantum computers. They have been shown to be advantageous in tasks such as implementing Toffoli gates, quantum Fourier transforms, and quantum error correction.
Our approach focuses on minimizing the number of MQ gate layers, combining many smaller interactions into larger, more efficient steps, thus significantly compressing the circuit’s depth. This reduces the resources needed and improves accuracy. Unlike traditional methods that minimize two-qubit gates, our method takes advantage of simultaneous interactions, even if the total number of pairwise interactions exceeds that in the original circuit.
For example, a three-qubit Toffoli gate normally requires six CNOT two-qubit gates, shown in the sketch:

But by using MQ gates it can be implemented with just three layers (orange frames), even though these realize 7 two-qubit interactions, the operation is significantly simplified:

Our compilation also makes use of the fact that CNOT gates that appear at the edges (beginning or end) of quantum circuits are unnecessary – they can be efficiently performed with classical computer before and after the operation of the quantum computer.
We utilize this to commute, that is ‘push’ and ‘pull’, CNOT gates to the edges of the circuits. In the sketch we plan to ‘pull’ all CNOT gates to the beginning (left side) of the circuit:
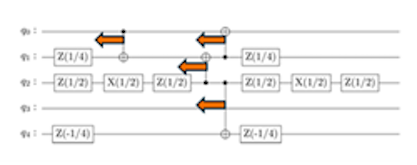
This is not a trivial task, as this commutation leaves a ‘wake’ of massive entanglement structures known as phase-gadgets(orange frames):

Formally, these phase-gadgets take the form of the many-body operation:
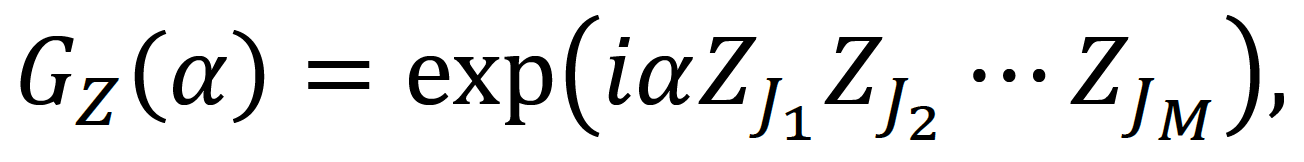
with α a user-defined many-body entanglement phase and J any subset of the qubit register (a similar expression exists with X-operators).
While phase gadgets are problematic for quantum computers based on two-qubit gates, they are easily implemented using MQ gates, at the cost of one MQ per phase gadget. This realization drives our Phase-gadget compiler, which, in turn, serves to further compress the quantum circuit.
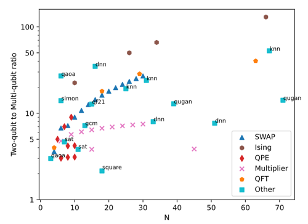
We test the performance of our compiler on a set of benchmark circuits (including but not limited to QASMBench, https://doi.org/10.1145/3550488).With circuits such as ‘Swap’ (blue), ‘Multiplier’ (orange) or ‘QPE’ (green,Quantum phase estimation), that can be formed for any qubit number, N. Others(red, see captions) are more specialized circuits. The figure shows the compression, that is the ratio between two-qubit gates and MQ gates used before we compile to phase-gadgets. Already huge gate compression is observed (left).On top of this we compile the circuits with the Phase-gadget compiler, yielding an even larger overall compression (right):

Showing a huge advantage. On average more than a 10X compression is observed.
While phase-gadgets are ‘economical’ in terms of MQ gates, they can require a lot of laser power to drive the trapped-ions qubits. This in turn leads to reduced performance, as many fundamental errors occur at high-power. The drive power of the phase gadgets can be efficiently reduced by ‘injecting’ a CNOT pair at the edge of the circuit and commuting one of the CNOTs to the other edge. This time the CNOT ‘wake’ is utilized to optimize the drive power:
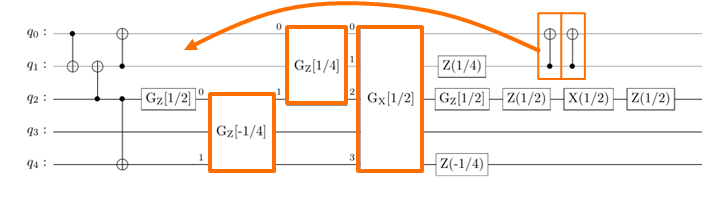
This is in fact an instance of the famous MaximumWeight Matching problem. We perform this optimization in parallel, that is weinject many CNOT pairs at once. This requires fast multiplication of large matrices. This task is well suited for GPUs – indeed, for medium and large circuits, GPU-accelerating this optimization step using the NVIDIA CUDA-Q platform reduces the compilation time by 10X.
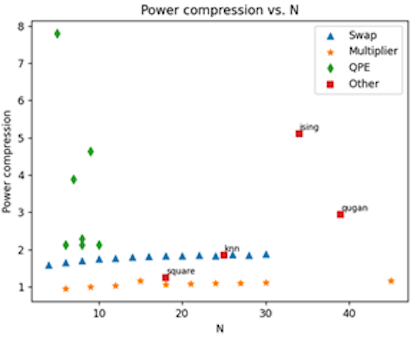
We test the overall power reduction, that is the ratio between the total power required for an implementation with two-qubit gates to that required with multi-qubit gates. As a result of the optimization, phase-gadgets do not require more power. In fact, for many instances power decreases, thus reducing both the circuit depth and drive power:
The reduction of circuit depth and drive power ultimately is translated to an improved performance. We estimate the performance boost of our compiled circuits. A simple estimate is formed by considering two-qubit gates implemented at a 99.9% success rate and calculating the probability of running an error-less circuit, F2Q. Similarly, we derive the multi-qubit gate error and calculate the probability of running an error-less instance of the phase-gadget compiled circuit, FMQ. The relative error reduction is then given by:
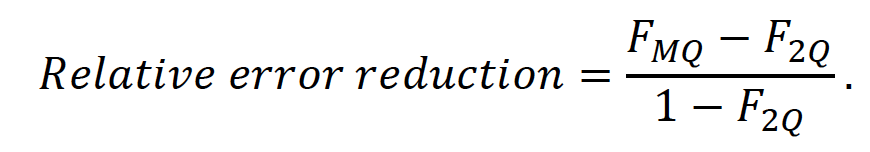
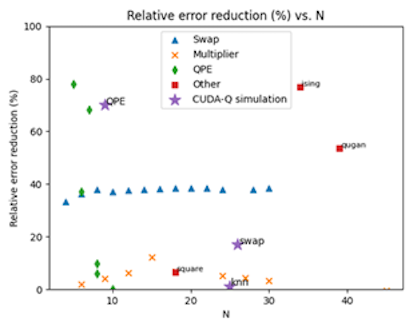
As shown below we observe a large boost in performance, with an average of 30% relative error reduction.
For selected circuits (QPE, knn, SWAP), we perform a more precise estimation by running up to 100,000 noise-injected realizations of the input and compiled circuits, and estimate their success probability using total variation distance. This computationally demanding task is executed using the NVIDIA CUDA-Q state simulation toolbox, running on anNVIDIA DGX H100. The resulting data (purple stars) closely matches our heuristic results.
In summary, we have shown that our Phase-gadget compiler leverages multi-qubit gates to reduce circuit depth by 10X and reduce errors by 30%. The compilation is performed on NVIDIA DGX H100GPUs and tested and verified using the CUDA-Q platform.